ボストン市の住宅価格をScikit-learnの重回帰分析で予測

はじめに

以前の記事では単回帰分析でボストンの住宅価格を予測しました。
今回は重回帰分析で予測してみたいと思います。
（ボストンの住宅価格データセットとデータの可視化は以前の記事を参照ください。）

AIや機械学習といった分野に興味がある方は以下の記事もおすすめですので、是非一度ご覧になってみてください。

・【初心者向け】AI（人工知能）について初心者が最初に知っておくべきこと

・フルタイムで働きながらCoursera ディープラーニング講座（1～4コース）を一ヶ月で受講した話

重回帰分析とは

単回帰分析では説明変数が一つのみでしたが、重回帰分析では説明変数が複数扱うことができます。
重回帰分析を式で表すと以下のようになります。

係数の確認

ボストン住宅価格データセットのどのカラム（係数）が説明変数に最も影響を与えたかを確認します。

import pandas as pd
from sklearn.datasets import load_boston

# ボストン市の住宅価格
dataset = load_boston()

df = pd.DataFrame(dataset.data, columns=dataset.feature_names)#説明変数
df['MEDV_PRICE'] = dataset.target #目的変数も追加

mlt_model = LinearRegression()
X_mlt = df.drop('MEDV_PRICE', 1) #説明変数
y_mlt = df["MEDV_PRICE"]
mlt_model.fit(X_mlt, y_mlt)

coeff_df = pd.DataFrame()
coeff_df["Features"] = df.columns[:-1]
coeff_df["Coefficient Estimate"] = mlt_model.coef_
print(coeff_df)

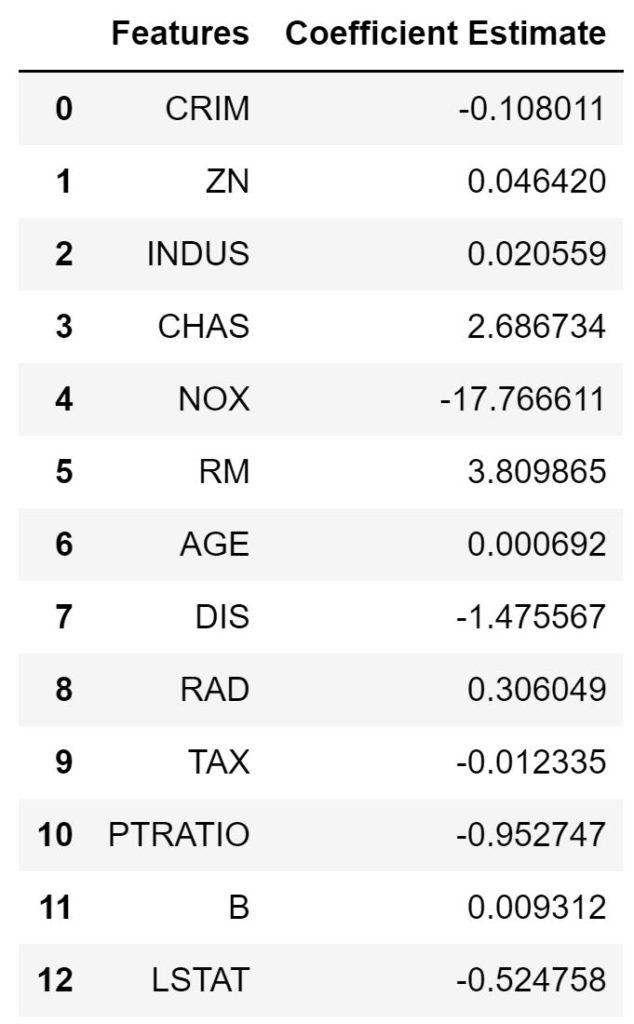
部屋数が最も大きく、説明変数に一番影響を与えることがわかります。

モデルの学習

訓練データとテストデータに分割して、モデルの学習を行います。

X_mlt_train, X_mlt_test, y_mlt_train, y_mlt_test = train_test_split(X_mlt, y_mlt, test_size=0.3, random_state=0)
mlt_lreg = LinearRegression()
mlt_lreg.fit(X_mlt_train, y_mlt_train)

予測精度の算出

最後に、決定係数による予測精度を算出してみましょう。

mlt_lreg.score(X_mlt_train, y_mlt_train)

オススメ書籍

・データ前処理の定番。データ分析を実務で使う人は手元に置いておきたい一冊です。

前処理大全[データ分析のためのSQL/R/Python実践テクニック]

・特徴量エンジニアリングについてわかりやすく書かれている良書です。
私も何度も見返しています。

機械学習のための特徴量エンジニアリング ―その原理とPythonによる実践 (オライリー・ジャパン)

スポンサーリンク