目次
はじめに
機械学習は最近ではすっかりメジャーな言葉になってきましたね。
機械学習やディープラーニングに興味があってこれから本格的に勉強していきたい方は下の記事もオススメです!
・【初心者向け】AI(人工知能)について初心者が最初に知っておくべきこと
・フルタイムで働きながらCoursera ディープラーニング講座(1~4コース)を一ヶ月で受講した話
さて、今回はscikit-learnのサンプルデータを使ってボストン市の住宅価格を予測してみました。
今回は、住居の平均部屋数と住宅価格の関係を使った単回帰分析でどこまで精度が出せるか検証してみます。
ボストン住宅価格のデータセット
データセットを読み込み、米国ボストン市郊外の地域別のデータを見てみましょう。
import pandas as pd from sklearn.datasets import load_boston # ボストン市の住宅価格 dataset = load_boston() # データフレームに変換 df = pd.DataFrame(dataset.data, columns=dataset.feature_names)#説明変数 df['MEDV_PRICE'] = dataset.target #目的変数も追加 df.head()
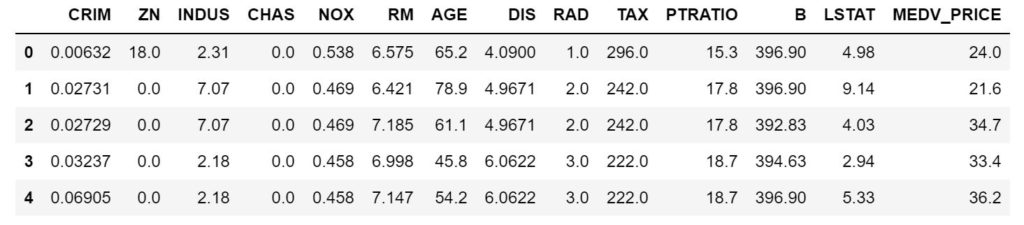
・カラム数は:14

データの可視化
予測モデルが最終的に算出する値となります。
#価格のヒストグラム
import matplotlib.pyplot as plt
plt.hist(dataset.target, bins=50)
plt.xlabel('Price in $1,000s')
plt.ylabel('Number of houses')
plt.grid()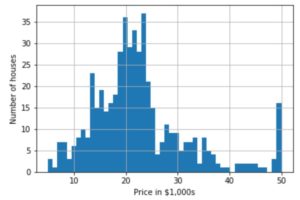
次に、今回着目する二つのパラメータ(平均部屋数と)の関係性を散布図にして確認してみましょう。
部屋の数が多くなるに従って住宅価格も上昇する傾向があることがわかります。
# 平均部屋数と住宅価格の散布図
plt.scatter(df['RM'], df['MEDV_PRICE'])
plt.xlabel('Average number of rooms [RM]') # X軸
plt.ylabel('Median Prices')
plt.grid()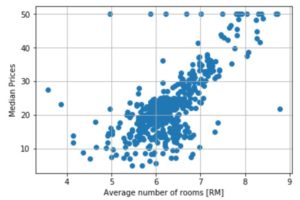
データの前処理
予測モデルを作る前のデータ処理を行います。
まずは平均部屋数を説明変数、住宅価格を目的変数とし、
Numpy形式の列ベクトルに変換しておきます。
import numpy as np from sklearn.linear_model import LinearRegression model = LinearRegression # 平均部屋数を変数X, 住宅価格を変数yに保存 X = df["RM"] y = df["MEDV_PRICE"] # 列ベクトル X = np.array(X).reshape(-1, 1) y = np.array(y).reshape(-1, 1)
次に、訓練データとテスト用データを7:3に分割します。
# 訓練データとテストデータに7:3に分割 from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
モデルの学習
sklearnの線形回帰モデルの一つを使って予測モデルを作ってみます。
# モデルの学習 from sklearn.linear_model import LinearRegression model = LinearRegression() model.fit(X_train, y_train)
予測精度の算出
予測精度の確認方法として、平均二乗誤差(MSE, Mean Squared Error)と決定関数(R2, R-squared, coefficient of determination)を使ってみたいと思います。
平均二乗誤差は、実際の値と予測値の絶対値の2乗を平均したものです。値が大きいほど誤差の多いモデルとなります。
決定関数は、モデルの当てはまりの良さを示す指標です。最も当てはまる場合は、1.0となります。
# 平均二乗誤差による予測精度算出
from sklearn.metrics import mean_squared_error
y_test_pred = model.predict(X_test) #テストデータを用いて目的変数を予測
y_train_pred = model.predict(X_train) #学習データに対する目的変数を予測
print('MSE train data: ', mean_squared_error(y_train, y_train_pred))
print('MSE test data: ', mean_squared_error(y_test, y_test_pred))![]()
・決定係数による予測結果
# 決定係数による予測精度算出
from sklearn.metrics import r2_score
print('r^2 train data: ', r2_score(y_train, y_train_pred))
print('r^2 test data: ', r2_score(y_test, y_test_pred))![]()
結果を見てもらうとわかる通り、単回帰分析ではあまり良い精度は出ませんでした。
データセットには部屋数以外にもたくさんのデータが用意されています。
次はそれらのデータも使って重回帰分析を試してみたいと思います。
オススメ書籍
・Python使ってデータ分析するならPandasは必須ですね。
そのPandasの使い方をわかりやすくまとめてられています。

Pythonデータ分析/機械学習のための基本コーディング! pandasライブラリ活用入門 impress top gearシリーズ
・これからデータサイエンスを本格的にやりたい人は、是非一冊は手元に置いておきたい良書です。

[第2版]Python 機械学習プログラミング 達人データサイエンティストによる理論と実践 (impress top gear)
