こんにちわ！やじろべえです。
今回は因果推論シリーズの第二弾として、バイアスのあるデータを疑似的に作り、その効果検証をしてみました。
因果推論第一弾（RCTによる効果検証）はこちらの記事をご覧下さいませ。
今回も教科書は下記の書籍を参考にしています。内容の多くが因果推論をビジネス利用する観点で書かれており、現場でデータ分析する人は読んでおいて損は無いと思います。
第一弾と同じように、データセットはMineThatData E-Mail Analytics And Data Mining Challenge datasetを使います。今回も検証の簡略化のため、女性向けのメール配信データは削除し、介入グループは男性向けメール配信ユーザーに限定します。
目次
データの読込みと女性向けメール配信レコードの削除
import pandas as pd
import numpy as np
from scipy import stats
df = pd.read_csv('./MineThatData_E-MailAnalytics.csv')
mens_df = df[df['segment'] != 'Womens E-Mail']
# 男性向けにメール配信があったユーザーにフラグ付け
mens_df['treatment'] = 0
mens_df['treatment'].where(mens_df['segment'] != 'Mens E-Mail', 1, inplace=True)
バイアスのあるデータの作成
効果検証入門
に書かれているように、メール配信を担当する担当者が購買傾向が一定以上あるユーザーに重点的にメール配信したと仮定します。そのような状況を再現するためのデータを作成します。
具体的には、メールが配信されていないグループには次の３つの条件のいずれかに該当するデータをランダムに半分選んで削除。一方でメールが配信されているグループは同じ条件に該当しないデータをランダムに半分選んで削除。
- 昨年の購入額が300より高い（history > 300）
- 最後の購入が6より小さい（recency < 6)
- 接触チャンネルが複数ある（channel = Multichannel）
# メール配信の担当者が購買傾向が一定以上あるユーザーに重点的にメール配信をした状況を再現するデータセットの作成 bias_rules = (mens_df['history'] > 300) | (mens_df['recency'] < 6) | (mens_df['channel'] == 'Multichannel') biased_df = pd.concat([ mens_df[(bias_rules) & (mens_df.treatment == 0)].sample(frac=0.5, random_state=1), mens_df[(bias_rules) & (mens_df.treatment == 1)], mens_df[(~bias_rules) & (mens_df.treatment == 0)], mens_df[(~bias_rules) & (mens_df.treatment == 1)].sample(frac=0.5, random_state=1) ], axis=0, ignore_index=True)
セレクションバイアスのあるデータの集計と有意差検定
まずはセレクションバイアスのあるデータの集計をします。
biased_df.groupby('treatment').agg(
conversion_rate=('conversion', 'mean'),
spend_mean=('spend', 'mean'),
count=('treatment', 'count')
)
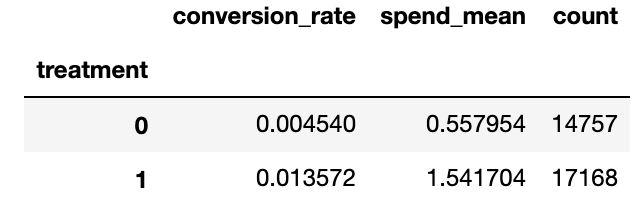
メールを配信したグループとしないグループでのconversion_rateの差はおよそ0.009、spendの差はおよそ0.98となり、いずれも第一弾の記事で検証したRCTの結果よりも大きくなっています。
次にwelchのt検定で統計的有意差を見てみます。
from scipy import stats mens_email_biased = biased_df[biased_df['treatment'] == 1] no_mail_biased = biased_df[biased_df['treatment'] == 0] stats.ttest_ind(mens_email_biased['spend'], no_mail_biased['spend'], equal_var=False) # Ttest_indResult(statistic=5.799473880787556, pvalue=6.722150409691524e-09)
二つのグループ間の平均の売上げの差は統計的に有意なものを示唆していることがわかりました。
また、p値はRCTでの検証結果よりも小さい値となっています。
セレクションバイアスによって割付られたデータは一見すると統計的有意差もあり、平均値での比較もそれらしい結果が出ましたが、この分析は意味のあるものとは思えなく、この結果で意思決定をするとリスクがあることがわかりました。
まとめ
効果検証入門を参考にして、バイアスのあるデータによる効果検証をpythonで確かめました。セレクションバイアスで得られたデータは一見すると最もらしい結果を返すので、分析する前にどのようにデータを入手するかといった実験のデザインも含めてしっかり考えなくてはいけないですね。
参考書籍
- 効果検証入門（正しい比較のための因果推論/計量経済学の基礎）
